When stacking two layers of 2D materials together with a twisted angle, the bandstructure, therefore the properties, of 2D materials will be modified due to the potential of superlattices and hybridization between two layers. In twisted graphene at very small twist angle of 0.1°, which we call marginally twisted bilayer graphene, the lattice reconstruction results in submicron-size triangular network as shown below.

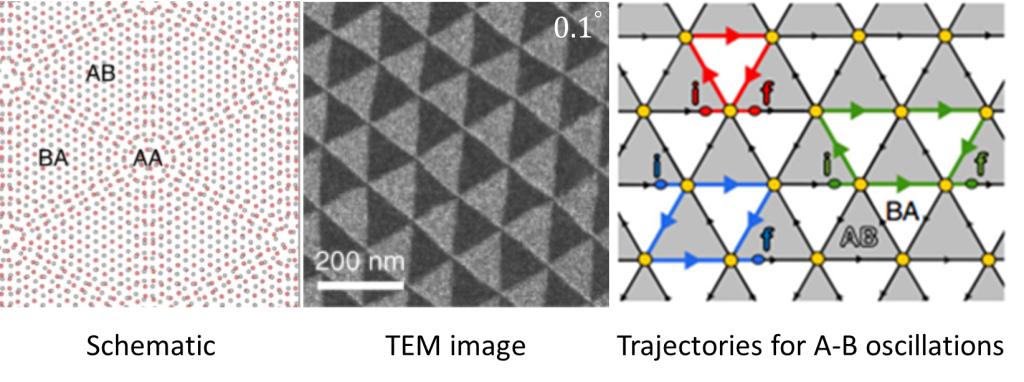
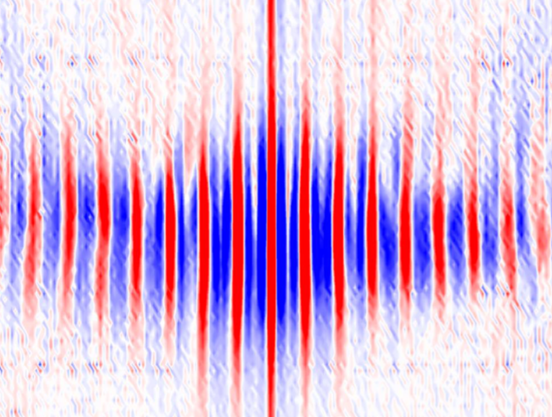
When propagating in such triangular network, electrons can only travel along the boundary of the triangular lattice under some condition. The interference of electrons in marginally twisted bilayer graphene results in the observation of Aharonov-Bohm oscillations as shown in the title image. These quantum oscillations are different from the usual Shunbikov-de Haas oscillations in several ways: the Aharonov-Bohm oscillations have a period in B not 1/B; they are independent on carrier densities; they are quite robust, persisting to temperatures above 100 K.

References:

[1] H. Yoo, et. al., “Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene”, Nature Materials, 18, 448-453, (2019).

[2] S.G. Xu, et. al., “Giant oscillations in a triangular network of one-dimensional states in marginally twisted graphene”, Nature Communications, 10, 4008, (2019).