Electron fluid in graphene

As an example of how useful 2D materials are, we have used h-BN encapsulated graphene heterostructures to find the long-sought Hall viscosity in fluid. In high-quality graphene, electrons can frequently collide with each other, bringing the system into hydrodynamic regime. Compared with classical fluids, one unique feature of such electron fluids is that time reversal symmetry can be simply broken by applying a small magnetic field. In this way, we succeeded to observe viscous Hall effect and experimentally measure Hall viscosity, which has been theoretically predicted in fluid dynamics for a long time, but not experimentally confirmed until now.  

References:

1.  A. I. Berdyugin*, S. G. Xu*, et. al. , “Measuring Hall viscosity of graphene’s electron fluid”, Science, 364(6436), 162-165, (2019).

2. M. Kim*, S. G. Xu*, et. al., “Control of electron-electron interaction in graphene by proximity screening”, Nature Communication, 11, 2339, (2020).

Twistronics

In 2D materials and their heterostructures, many experimental knobs, such as carrier density, electrical displacement, pressure, etc., can be tuned to explore and control their properties. One controllable knob is the twisted angle, leading to the concept of twistronics. By tuning the twisted angle between two van der Waals layers, one can tune the strength of interlayer coupling and the hybridization of band structure, thus significantly modifying their electronic properties.

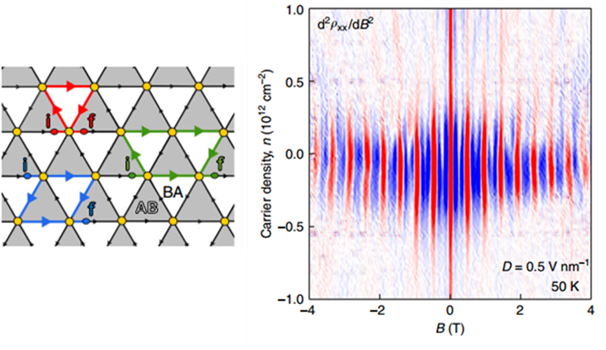
Taking graphene for instance, the physical pictures are totally different in various angle regime: at twisted angle around or larger than 2°, the band spectrum consists of two uncoupled Dirac cone; near magic angle (~1.1°), strong interlayer hybridization results in a flat band and strong correlations emerge; at marginally twisted angle below 1°, atomic lattice reconstruction leads to the formation of topological one-dimensional conducting channel.

How twisted angles affect other 2D materials is still under exploration. We are trying to contribute to this emerging field.

References:

1. S. G. Xu, et. al., “Giant oscillations in a triangular network of one-dimensional states in marginally twisted graphene”, Nature Communications, 10, 4008, (2019).

2. A. I. Berdyugin, B. Tsim, P. Kumaravadivel, S. G. Xu, et. al., “Minibands in twisted bilayer graphene probed by magnetic focusing”, Science Advances, 6, 16, eaay7838, (2020).

3. S.G. Xu, et. al., “Tunable van Hove singularities and correlated states in twisted monolayer-bilayer graphene”, Nature Physics, https://doi.org/10.1038/s41567-021-01172-9, (2021).

Stacking order matters

The stacking order of individual layers can also significantly change the band structure of 2D materials. For example, there are two kinds of stacking order in graphite: Bernal stacking (also known as ABA stacking) and rhombohedral stacking (or ABC stacking). Rhombohedral stacking in graphite is a metastable state and can be spontaneously converted to the stable Bernal stacking. Even so, we successfully fabricated high-quality rhombohedral multilayer graphite devices with various thickness up to 50 layers by van der Waals assembly technique. After achieving this, we observed the flat band in the surface states of rhombohedral graphite, which hosts many exotic physics.

Reference:  

Y.M. Shi*, S.G. Xu*, et. al., “Electronic phase separation in multilayer rhombohedral graphite”, Nature, 584, 210-214, (2020).

Valleytronics in transition metal dichalcogenides

2D materials consist of a large family, with various properties covering from metals (graphene), insulators (h-BN), semiconductors (MoS₂), superconductors (NbSe₂), topological insulators (Bi₂Se₃), ferromagnets (CrI₃), etc.. This allows us to design novel devices with unique properties. One kind of promising 2D materials is transition metal dichalcogenides (TMDCs), such as MoS₂, WSe₂. In monolayer TMDCs, the lack of inversion symmetry makes it possible to manipulate valley degree of freedom. Using valley as medium to store and carry information can lead to new conceptual devices known as valleytronics, similar to traditional electronics by using charge to process information. We can also control contributed valleys by layer number and Fermi level tuning. In this way, we observed several unusual quantum states in Γ valley and Q valley of TMDCs.

Reference:  

1. S.G. Xu, et. al., “Odd-integer quantum hall states and giant spin susceptibility in p-type few-layer WSe₂”, Physical Review Letters, 118, 067702, (2017).

2. Z.F. Wu*, S.G. Xu*, et. al., “Even-odd layer-dependent magnetotransport of high-mobility Q-valley electrons in transition metal disulfides”, Nature Communications, 7, 12955, (2016).

3. S.G Xu*, et. al., “Universal low-temperature Ohmic contacts for quantum transport in transition metal dichalcogenides”, 2D materials, 3, 021007, (2016).